what energy systems contribute to the internal energy u
Internal free energy
| Thermodynamic potentials | |
|---|---|
| Internal free energy | U(S,V) |
| Helmholtz free energy | A(T,V) = U − T Southward |
| Enthalpy | H(S,p) = U + P 5 |
| Gibbs free energy | M(T,p) = U + P V − T S |
| edit | |
In thermodynamics, the internal energy of a thermodynamic arrangement, or a body with well-defined boundaries, denoted byU, or sometimesDue east, is the total of the kinetic energy due to the move of molecules (translational, rotational, vibrational) and the potential energy associated with the vibrational and electric energy of atoms within molecules or crystals. Information technology includes the energy in all the chemical bonds, and the energy of the gratuitous, conduction electrons in metals.
The internal energy is a thermodynamic potential and for a closed thermodynamic system held at constant entropy, information technology will be minimized.
One tin as well summate the internal energy of electromagnetic or blackbody radiation. It is a state role of a system, an extensive quantity. The SI unit of energy is the joule although other historical, conventional units are all the same in use, such as the (pocket-sized and big) calorie for rut.
Additional recommended noesis
Contents
- 1 Overview
- 2 Limerick
- 3 The first law of thermodynamics
- 4 Expressions for the internal energy
- v References
- six Meet likewise
Overview
Internal free energy does not include the translational or rotational kinetic free energy of a body every bit a whole. It likewise does not include the relativistic mass-energy equivalent E =mc 2. It excludes any potential energy a body may take because of its location in external gravitational or electrostatic field, although the potential energy information technology has in a field due to an induced electric or magnetic dipole moment does count, equally does the free energy of deformation of solids (stress-strain).
The principle of equipartition of energy in classical statistical mechanics states that each molecular degree of liberty receives 1/twokT of energy, a result which was modified when quantum mechanics explained certain anomalies; east.grand., in the observed specific heats of crystals (when hν >kT). For monatomic helium and other noble gases, the internal energy consists only of the translational kinetic energy of the individual atoms. Monatomic particles, of course, exercise not (sensibly) rotate or vibrate, and are not electronically excited to higher energies except at very high temperatures.
From the standpoint of statistical mechanics, the internal energy is equal to the ensemble average of the total energy of the organization.
Composition
Internal energy – the sum of all microscopic forms of energy of a organisation. It is related to the molecular structure and the degree of molecular activity and may be viewed as the sum of kinetic and potential energies of the molecules; it is comprised of the following types of energies:[one]
| Type | Composition of Internal Energy (U) |
|---|---|
| Sensible energy | the portion of the internal energy of a arrangement associated with kinetic energies (molecular translation, rotation, and vibration; electron translation and spin; and nuclear spin) of the molecules. |
| Latent energy | the internal energy associated with the phase of a organisation. |
| Chemical energy | the internal energy associated with the atomic bonds in a molecule. |
| Nuclear free energy | the tremendous corporeality of energy associated with the stiff bonds within the nucleus of the atom itself. |
| Energy interactions | those types of energies not stored in the system (e.g. heat transfer, mass transfer, and work), but which are recognized at the organisation boundary as they cross it, which represent gains or losses by a system during a process. |
| Thermal energy | the sum of sensible and latent forms of internal energy. |
The first constabulary of thermodynamics
The internal energy is substantially defined past the first police of thermodynamics which states that free energy is conserved:
where
- ΔU is the change in internal energy of a system during a procedure.
- Q is rut added to a system (measured in joules in SI); that is, a positive value for Q represents heat menses into a system while a negative value denotes oestrus flow out of a organization.
- W is the mechanical work washed on a system (measured in joules in SI)
- W' is free energy added by all other processes
The first law may be equivalently in infinitesimal terms as:
where the terms now represent minute amounts of the respective quantities. The d earlier the internal energy function indicates that information technology is an exact differential. In other words it is a state function or a value which can be assigned to the arrangement. On the other hand, the δ'southward before the other terms indicate that they draw increments of free energy which are non state functions just rather they are processes by which the internal free energy is changed. (Meet the discussion in the first law article.)
From a microscopic point of view, the internal energy may be constitute in many different forms. For a gas it may consist nearly entirely of the kinetic energy of the gas molecules. It may besides consist of the potential energy of these molecules in a gravitational, electric, or magnetic field. For any textile, solid, liquid or gaseous, it may too consist of the potential energy of allure or repulsion between the individual molecules of the material.
Expressions for the internal energy
Strictly speaking, the internal energy cannot be precisely measured. This is considering only changes in the internal energy can exist measured, and the total internal energy of a given arrangement is the difference between the internal energy of the system and the internal energy of the same organisation at absolute zippo temperature. Since accented zero cannot be attained, the total internal energy cannot exist precisely measured. The same is true of other thermodynamic parameters such every bit entropy and the chemical potential.
The internal energy may exist expressed in terms of other thermodynamic parameters. Each term is equanimous of an intensive variable (a generalized force) and its cohabit infinitesimal extensive variable (a generalized displacement).
For instance, for a non-viscous fluid, the mechanical work done on the system may be related to the pressure p and volume V. The pressure is the intensive generalized strength, while the volume is the extensive generalized displacement:
Taking the default direction of work, W , to be from the working fluid to the surroundings,
-
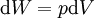 .
. - p is the pressure
- Five is the volume
Taking the default direction of heat transfer, Q , to be into the working fluid and assuming a reversible process, we have
-
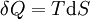 .
. - T is temperature
- S is entropy
Although the internal energy is not exactly measurable, information technology may exist expressed in terms of other similarly unmeasurable quantities. Using the above 2 equations in the first law of thermodynamics to construct ane possible expression for the internal energy of a closed arrangement gives:
The internal energy function may be written as U(S,V) in which case information technology follows that, since U, S, and V are all-encompassing
From Euler'due south homogeneous office theorem we may now write the internal free energy as:
If the (non-viscous) fluid gains energy from the improver of particles, we add the chemical energy term:
-
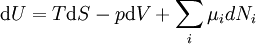
-
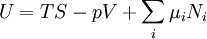 .
. - μ i is the chemic potential of chemical species i . It is an intensive variable.
- N i is the particle number of chemic species i. It is an extensive variable.
For an elastic substance the mechanical term must be replaced by the more full general expression involving the stress σ i j and strain 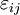 . The infinitesimal statement is:
. The infinitesimal statement is:
where Einstein notation has been used for the tensors, in which there is a summation over all repeated indices in the product term. For a linearly elastic material, the stress tin be related to the strain by:
and the Euler theorem yields for the internal energy (Landau & Lifshitz 1986):
References
- Alberty, R. A. (2001). "Utilize of Legendre transforms in chemic thermodynamics". Pure Appl. Chem. Vol. 73 (8): 1349–1380.
- Lewis, Gilbert Newton; Randall, Merle: Revised by Pitzer, Kenneth S. & Brewer, Leo (1961). Thermodynamics, 2nd Edition, New York, NY USA: McGraw-Hill Book Co.. ISBN 0-07-113809-9.
- Landau, L. D.; Lifshitz, E. M. (1986). Theory of Elasticity (Course of Theoretical Physics Book seven), (Translated from Russian by J.B. Sykes and W.H. Reid), Tertiary ed., Boston, MA: Butterworth Heinemann. ISBN 0-7506-2633-Ten.
- ^ Cengel, Yungus, A.; Boles, Michael (2002). Thermodynamics - An Engineering Approach, 4th ed.. McGraw-Hill, 17-18. ISBN 0-07-238332-one.
See too
- Calorimetry
- Thermodynamic equations
- Thermodynamic potentials
- Gibbs costless energy
Source: https://www.chemeurope.com/en/encyclopedia/Internal_energy.html
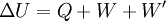
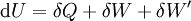
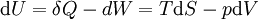
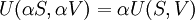
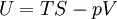
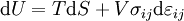
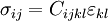
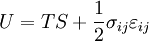
Post a Comment for "what energy systems contribute to the internal energy u"